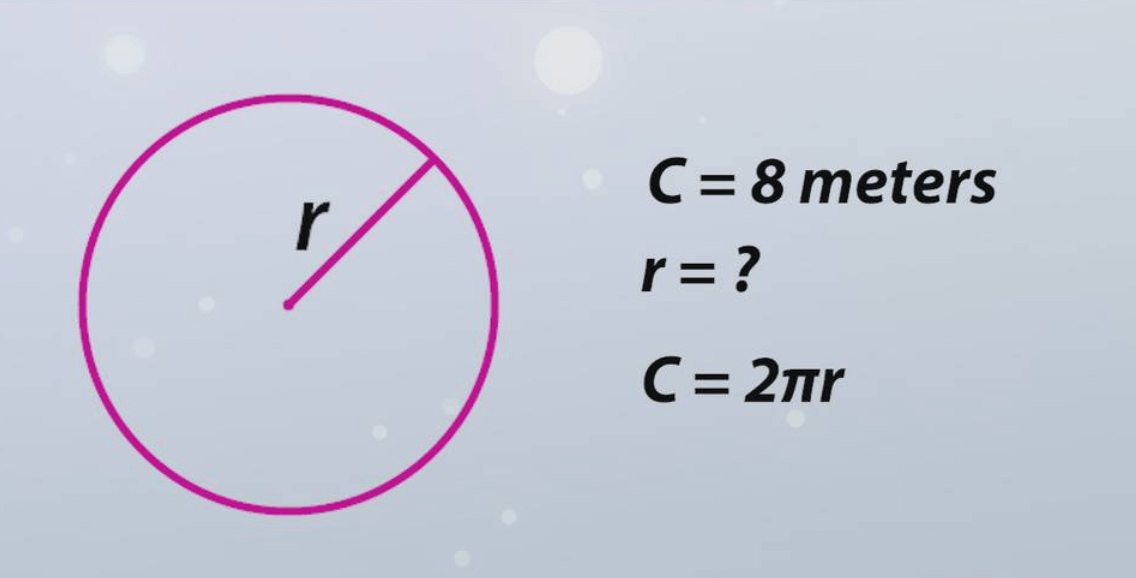
What Is the Radius of a Circle?
But what is the radius of a circle and why is it so important in understanding circular structures?
Core Meaning
It is one of the most important measurements in circle geometry because it helps determine other aspects of the circle such as the diameter, circumference, and area.
Visual Understanding
To better understand what is the radius of a circle, imagine a coin. If you draw a line from the center of the coin to any point on its curved edge, that line represents the radius. No matter which point on the edge you choose, the distance from the center remains the same.
This equidistance from the center is what defines the circle.
Relation to Diameter
The diameter of a circle is a straight line that passes through the center and touches two points on the edge.
Formula:
Diameter (d) = 2 × Radius (r)
This simple relationship allows you to find the radius if you know the diameter:
Radius = Diameter ÷ 2
So, if a circle has a diameter of 10 cm, then the radius is 5 cm.
See also: How to Maximize Deductions on Your T2 Corporation Income Tax Return in Toronto
Formula Applications
Knowing what is the radius of a circle is crucial in applying various mathematical formulas. Here are a few important ones:
1. Circumference:
C = 2πr
Where π is a constant (approximately 3.14159) and r is the radius.
2. Area:
The area is the amount of space enclosed within the circle.
A = πr²
Both of these formulas show how central the radius is in determining the size and boundary of a circle.
Units of Measurement
The radius, like any other length, is measured in units such as centimeters, meters, inches, or feet, depending on the context. In mathematics, the unit is usually left abstract, but in engineering or real-world measurements, choosing the correct unit is essential.
Finding the Radius
1. If You Know the Diameter:
Radius = Diameter ÷ 2
2. If You Know the Circumference:
Radius = Circumference ÷ (2π)
3. If You Know the Area:
Radius = √(Area ÷ π)
In each of these cases, the radius can be isolated by rearranging the standard circle formulas.
Importance in Geometry
Understanding what is the radius of a circle plays a foundational role in geometry. Without the radius, it’s impossible to solve circle-related problems in algebra, trigonometry, or calculus. For example, in coordinate geometry, the equation of a circle is written as:
Role in Real Life
The concept of the radius is not just theoretical. Consider the following examples:
1. Wheels and Tires:
Manufacturers measure the radius to ensure the wheels fit vehicles properly.
2. Construction and Architecture:
Engineers use the radius to design circular elements like domes, arches, and columns.
3. Art and Design:
Designers use the radius in drawing curves, creating circular logos, and designing layouts.
4. Technology:
Many sensors and devices use circular elements where radius calculations help ensure precision, such as in lenses and circuit boards.
Radius in Nature
Nature also showcases the radius in action. When you drop a pebble into water, circular ripples spread out from the impact point. Each ripple has a radius that increases over time, illustrating the expanding nature of energy or motion.
In biology, the radius plays a role in understanding cellular structures, the cross-section of trees, and the growth patterns of shells and organisms.
Symbolism and Conceptual Meaning
In addition to its mathematical meaning, the radius can symbolize connection, reach, and influence. In strategic planning or emergency response, people often speak of a radius of action, defining a circular zone from a central location.
Similarly, in social science or urban planning, radius is used to define how far a resource or facility should be accessible—such as the service radius of a hospital or school.
Summary
So, what is the radius of a circle? It is more than just a distance—it’s the key to unlocking the full geometry and function of one of the most elegant shapes in mathematics. Whether in theory, real life, or natural patterns, the radius defines how a circle behaves, how large it is, and how it relates to the world around it.
From calculating area and circumference to solving complex engineering problems, the radius remains at the center of circular analysis. Understanding and using the radius opens doors to geometry, science, technology, and everyday logic.



